vwood github email

IDF

28 April 2012

In Information Retrieval we are often asked to measure how relevant words are. The Inverse Document Frequency of a word is part of a simple measure (tfidf) that does this. Inverse Document Frequency lowers the value of words which occur often. These are less specific (compare ‘the’ to ‘lithographic’) and we downplay them.

So here is IDF:

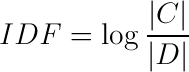
IDF=log(\|C\|/\|D\|)

Where D is the set of docs containing a chosen word in the collection of documents, C. |x| takes the size of the set x. The logarithm is used to decrease the magnitude of the number. So the IDF portion of the formula does not out weigh the Term Frequency half. Normally it would range from the number of documents in the collection (assuming we discount the infinite case for words not in the collection.) to 1 for a word that occurs in every document.

I thought to myself, this looks ‘informationy.’ It has a logarithm of a ratio. So to make it more so, let’s set the base to 21:

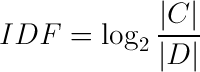
IDF=log2(\|C\|/\|D\|)

Furthermore, information theory is often full of probabilities, so if we replace the size of those sets with some probabilities:

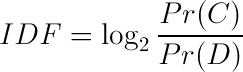
IDF=log2(Pr(C)/Pr(D))

What are those probabilities? Remembering that we are dealing with scores for a single word, they should be the probability the word occurs in either the collection, or a document. So let’s assume one for the collection probability (again ignoring the case where the word does not occur at all.)

Pr(C)=1

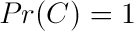
The probability of a particular word occuring a random document is simply the number of documents with the word over the number of documents:

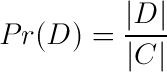
Pr(D)=\|D\|/\|C\|

So it turns out we were using the probabilities after all. Consider the following formula:

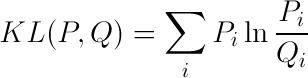
Kullback Leibler Divergence

This is an information measure called the Kullback-Leibler Divergence. This is an information measure of the difference between two probability distributions. In our case we are summing over a single case. When the word occurs. In an actual search engine tf-idf would be summed over all the words in a query. So IDF is the Kullback-Leibler Divergence where P is the collection and Q the set of documents containing our word.

  1. I have since realised that Kullback-Leibler uses the natural logarithm, my bad. The base of the logarithm for IDF (as far as I can tell) is ill-defined (possibly due to the many versions of IDF) so we could justify a natural base just as well. ↩